Fatou's theorem
In complex analysis, Fatou's theorem, named after Pierre Fatou, is a statement concerning holomorphic functions on the unit disk and their pointwise extension to the boundary of the disk.
Motivation and statement of theorem
If we have a holomorphic function  defined on the open unit disk
defined on the open unit disk  , it is reasonable to ask under what conditions we can extend this function to the boundary of the unit disk. To do this, we can look at what the function looks like on each circle inside the disk centered at 0, each with some radius
, it is reasonable to ask under what conditions we can extend this function to the boundary of the unit disk. To do this, we can look at what the function looks like on each circle inside the disk centered at 0, each with some radius  . This defines a new function on the circle
. This defines a new function on the circle  , defined by
, defined by  , where
, where ![S^{1}:=\{e^{i\theta}:\theta\in[0,2\pi]\}=\{z\in \mathbb{C}:|z|=1\}](../I/m/613e175b7140f282fa3d2c39907d206b.png) . Then it would be expected that the values of the extension of
. Then it would be expected that the values of the extension of  onto the circle should be the limit of these functions, and so the question reduces to determining when
onto the circle should be the limit of these functions, and so the question reduces to determining when  converges, and in what sense, as
converges, and in what sense, as  , and how well defined is this limit. In particular, if the
, and how well defined is this limit. In particular, if the  of these
of these  are well behaved, we have an answer:
are well behaved, we have an answer:
- Theorem: Let
 be a holomorphic function such that
be a holomorphic function such that
Then  converges to some function
converges to some function  pointwise almost everywhere and in
pointwise almost everywhere and in  . That is,
. That is,
- and
-
- for almost every
![\theta\in [0,2\pi]](../I/m/b1194bd0172849450c424366d14501a0.png) .
.
Now, notice that this pointwise limit is a radial limit. That is, the limit being taken is along a straight line from the center of the disk to the boundary of the circle, and the statement above hence says that
for almost every 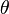 . The natural question is, now with this boundary function defined, will we converge pointwise to this function by taking a limit in any other way? That is, suppose instead of following a straight line to the boundary, we follow an arbitrary curve
. The natural question is, now with this boundary function defined, will we converge pointwise to this function by taking a limit in any other way? That is, suppose instead of following a straight line to the boundary, we follow an arbitrary curve  converging to some point
converging to some point  on the boundary. Will
on the boundary. Will  converge to
converge to  ? (Note that the above theorem is just the special case of
? (Note that the above theorem is just the special case of 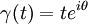 ).
It turns out that the curve
).
It turns out that the curve  needs to be nontangential, meaning that the curve does not approach its target on the boundary in a way that makes it tangent to the boundary of the circle. In other words, the range of
needs to be nontangential, meaning that the curve does not approach its target on the boundary in a way that makes it tangent to the boundary of the circle. In other words, the range of  must be contained in a wedge emanating from the limit point. We summarize as follows:
must be contained in a wedge emanating from the limit point. We summarize as follows:
- Definition: Let
 be a continuous path such that
be a continuous path such that  . Define
. Define
- and
- That is,
 is the wedge inside the disk with angle
is the wedge inside the disk with angle  : whose axis passes between
: whose axis passes between  and zero. We say that
and zero. We say that 
- converges nontangentially to
 , or that it is a nontangential limit, : if there exists
, or that it is a nontangential limit, : if there exists  such that
such that  is contained in
is contained in  and
and  .
.
- Fatou's theorem: Let
 . Then for almost all
. Then for almost all ![\theta\in[0,2\pi]](../I/m/b1194bd0172849450c424366d14501a0.png) ,
, 
- for every nontangential limit
 converging to
converging to  , where
, where  is defined as above.
is defined as above.
Discussion
- The proof utilizes the symmetry of the Poisson kernel using the Hardy–Littlewood maximal function for the circle.
- The analogous theorem is frequently defined for the Hardy space over the upper-half plane and is proved in much the same way.
See also
References
- John B. Garnett, Bounded Analytic Functions, (2006) Springer-Verlag, New York
- Walter Rudin. Real and Complex Analysis (1987), 3rd Ed., McGraw Hill, New York.
- Elias Stein, Singular integrals and differentiability properties of functions (1970), Princeton University Press, Princeton.


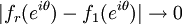

![\Gamma_{\alpha}=\{z:\arg z\in [\pi-\alpha,\pi+\alpha]\}](../I/m/a096091a41a74a814bdd2822515f1bf9.png)
