HPO formalism

The History Projection Operator (HPO) formalism is an approach to temporal quantum logic developed by Chris Isham. It deals with the logical structure of quantum mechanical propositions asserted at different points in time.

Introduction

In standard quantum mechanics a physical system is associated with a Hilbert space $\mathcal{H}$ . States of the system at a fixed time are represented by normalised vectors in the space and physical observables are represented by Hermitian operators on $\mathcal{H}$ .

A physical proposition $\,P$ about the system at a fixed time can be represented by a projection operator $\hat{P}$ on $\mathcal{H}$ (See quantum logic). This representation links together the lattice operations in the lattice of logical propositions and the lattice of projection operators on a Hilbert space (See quantum logic).

The HPO formalism is a natural extension of these ideas to propositions about the system that are concerned with more than one time.

History Propositions

Homogeneous Histories

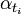A homogeneous history proposition $\,\alpha$ is a sequence of single-time propositions $\alpha_{t_i}$ specified at different times $t_1 < t_2 < \ldots < t_n$ . These times are called the temporal support of the history. We shall denote the proposition $\,\alpha$ as $(\alpha_1,\alpha_2,\ldots,\alpha_n)$ and read it as

" $\alpha_{t_1}$ at time $t_1$ is true and then $\alpha_{t_2}$ at time $t_2$ is true and then $\ldots$ and then $\alpha_{t_n}$ at time $t_n$ is true"

Inhomogeneous Histories

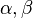Not all history propositions can be represented by a sequence of single-time propositions are different times. These are called inhomogeneous history propositions. An example is the proposition $\,\alpha$ OR $\,\beta$ for two homogeneous histories $\,\alpha, \beta$ .

History Projection Operators

The key observation of the HPO formalism is to represent history propositions by projection operators on a history Hilbert space. This is where the name "History Projection Operator" (HPO) comes from.

For a homogeneous history $\alpha = (\alpha_1,\alpha_2,\ldots,\alpha_n)$ we can use the tensor product to define a projector

$\hat{\alpha}:= \hat{\alpha}_{t_1} \otimes \hat{\alpha}_{t_2} \otimes \ldots \otimes \hat{\alpha}_{t_n}$

where $\hat{\alpha}_{t_i}$ is the projection operator on $\mathcal{H}$ that represents the proposition 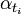$\alpha_{t_i}$ at time $t_i$ .

This $\hat{\alpha}$ is a projection operator on the tensor product "history Hilbert space" $H = \mathcal{H} \otimes \mathcal{H} \otimes \ldots \otimes \mathcal{H}$

Not all projection operators on $H$ can be written as the sum of tensor products of the form $\hat{\alpha}$ . These other projection operators are used to represent inhomogeneous histories by applying lattice operations to homogeneous histories.

Temporal Quantum Logic

Representing history propositions by projectors on the history Hilbert space naturally encodes the logical structure of history propositions. The lattice operations on the set of projection operations on the history Hilbert space $H$ can be applied to model the lattice of logical operations on history propositions.

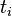If two homogeneous histories $\,\alpha$ and $\,\beta$ don't share the same temporal support they can be modified so that they do. If $\,t_i$ is in the temporal support of $\,\alpha$ but not $\,\beta$ (for example) then a new homogeneous history proposition which differs from $\,\beta$ by including the "always true" proposition at each time 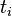$\,t_i$ can be formed. In this way the temporal supports of 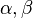$\,\alpha, \beta$ can always be joined together. What shall therefore assume that all homogeneous histories share the same temporal support.

We now present the logical operations for homogeneous history propositions $\,\alpha$ and $\,\beta$ such that $\hat{\alpha} \hat{\beta} = \hat{\beta}\hat{\alpha}$

Conjunction (AND)

If 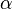$\alpha$ and $\beta$ are two homogeneous histories then the history proposition " $\,\alpha$ and $\,\beta$ " is also a homogeneous history. It is represented by the projection operator

$\widehat{\alpha \wedge \beta}:= \hat{\alpha} \hat{\beta}$ $(= \hat{\beta} \hat{\alpha})$

Disjunction (OR)

If 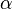$\alpha$ and $\beta$ are two homogeneous histories then the history proposition " $\,\alpha$ or $\,\beta$ " is in general not a homogeneous history. It is represented by the projection operator

$\widehat{\alpha \vee \beta}:= \hat{\alpha} + \hat{\beta} - \hat{\alpha}\hat{\beta}$

Negation (NOT)

The negation operation in the lattice of projection operators takes $\hat{P}$ to

$\neg \hat{P} := \mathbb{I} - \hat{P}$

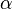where $\mathbb{I}$ is the identity operator on the Hilbert space. Thus the projector used to represent the proposition $\neg \alpha$ (i.e. "not $\alpha$ ") is

$\widehat{\neg \alpha}:= \mathbb{I} - \hat{\alpha}$

where $\mathbb{I}$ is the identity operator on the history Hilbert space.

Example: Two-time history

As an example, consider the negation of the two-time homogeneous history proposition $\,\alpha = (\alpha_1, \alpha_2)$ . The projector to represent the proposition $\neg \alpha$ is

$\widehat{\neg \alpha} = \mathbb{I} \otimes \mathbb{I} - \hat{\alpha}_1 \otimes \hat{\alpha}_2$ $= (\mathbb{I} - \hat{\alpha}_1) \otimes \hat{\alpha}_2 + \hat{\alpha}_1 \otimes (\mathbb{I} - \hat{\alpha}_2) + (\mathbb{I} - \hat{\alpha}_1) \otimes (\mathbb{I} - \hat{\alpha}_2)$

The terms which appear in this expression:

$(\mathbb{I} - \hat{\alpha}_1) \otimes \hat{\alpha}_2$
$\hat{\alpha}_1 \otimes (\mathbb{I} - \hat{\alpha}_2)$
$(\mathbb{I} - \hat{\alpha}_1) \otimes (\mathbb{I} - \hat{\alpha}_2)$ .

can each be interpreted as follows:

$\,\alpha_1$ is false and $\,\alpha_2$ is true
$\,\alpha_1$ is true and $\,\alpha_2$ is false
both $\,\alpha_1$ is false and $\,\alpha_2$ is false

These three homogeneous histories, joined together with the OR operation, include all the possibilities for how the proposition " $\,\alpha_1$ and then $\,\alpha_2$ " can be false. We therefore see that the definition of $\widehat{\neg \alpha}$ agrees with what the proposition $\neg \alpha$ should mean.

References

C.J. Isham, Quantum Logic and the Histories Approach to Quantum Theory, J.Math.Phys. 35 (1994) 2157-2185, arXiv:gr-qc/9308006v1

This article is issued from Wikipedia - version of the 3/29/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.