Kuratowski's free set theorem
Kuratowski's free set theorem, named after Kazimierz Kuratowski, is a result of set theory, an area of mathematics. It is a result which has been largely forgotten for almost 50 years, but has been applied recently in solving several lattice theory problems, such as the congruence lattice problem.
Denote by ![[X]^{<\omega}](../I/m/92f70898d873a38faa490813a8012682.png) the set of all finite subsets of a set
the set of all finite subsets of a set 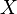 . Likewise, for a positive integer
. Likewise, for a positive integer 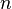 , denote by
, denote by ![[X]^n](../I/m/1c6c1f5813491c2d859b54fa4de8c4c6.png) the set of all
the set of all 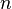 -elements subsets of
-elements subsets of 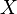 . For a mapping
. For a mapping ![\Phi\colon[X]^n\to[X]^{<\omega}](../I/m/ba26cc498a678f652c02220fb99514e6.png) , we say that a subset
, we say that a subset 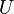 of
of 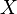 is free (with respect to
is free (with respect to  ), if for any
), if for any 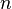 -element subset
-element subset 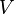 of
of 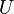 and any
and any  ,
,  ,. Kuratowski published in 1951 the following result, which characterizes the infinite cardinals of the form
,. Kuratowski published in 1951 the following result, which characterizes the infinite cardinals of the form  .
.
The theorem states the following. Let 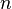 be a positive integer and let
be a positive integer and let 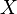 be a set. Then the cardinality of
be a set. Then the cardinality of 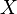 is greater than or equal to
is greater than or equal to  if and only if for every mapping
if and only if for every mapping  from
from ![[X]^n](../I/m/1c6c1f5813491c2d859b54fa4de8c4c6.png) to
to ![[X]^{<\omega}](../I/m/92f70898d873a38faa490813a8012682.png) ,
there exists an
,
there exists an  -element free subset of
-element free subset of 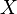 with respect to
with respect to  .
.
For  , Kuratowski's free set theorem is superseded by Hajnal's set mapping theorem.
, Kuratowski's free set theorem is superseded by Hajnal's set mapping theorem.
References
- P. Erdős, A. Hajnal, A. Máté, R. Rado: Combinatorial Set Theory: Partition Relations for Cardinals, North-Holland, 1984, pp. 282–285.
- C. Kuratowski, Sur une caractérisation des alephs, Fund. Math. 38 (1951), 14–17.
- John C. Simms (1991) "Sierpiński's theorem", Simon Stevin 65: 69–163.