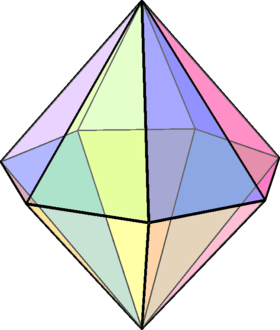
Octagonal bipyramid
| Octagonal bipyramid | |
|---|---|
 | |
| Type | bipyramid |
| Schläfli symbol | { } + {8} |
| Coxeter diagram | |
| Faces | 16 triangles |
| Edges | 24 |
| Vertices | 10 |
| Face configuration | V4.4.8 |
| Symmetry group | D8h, [8,2], (*228), order 32 |
| Rotation group | D8, [8,2]+, (228), order 16 |
| Dual | octagonal prism |
| Properties | convex, face-transitive |
The octagonal bipyramid is one of the infinite set of bipyramids, dual to the infinite prisms. If an octagonal bipyramid is to be face-transitive, all faces must be isosceles triangles.
Images
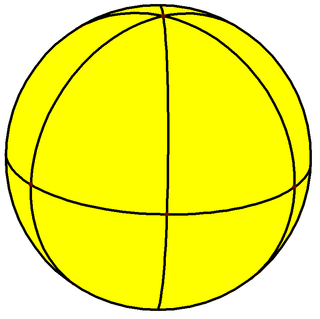
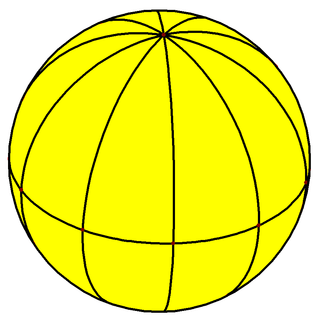
It can be drawn as a tiling on a sphere which also represents the fundamental domains of [4,2], *422 symmetry:
Related polyhedra
| Polyhedron |  |
 |
 |
 |
 |
 | |||
|---|---|---|---|---|---|---|---|---|---|
| Coxeter | |||||||||
| Tiling |  |
 |
 |
 |
 |
 |
 | ||
| Config. | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 |
| *n42 symmetry mutation of omnitruncated tilings: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *n42 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | |
| Omnitruncated figure |
 4.8.4 |
 4.8.6 |
 4.8.8 |
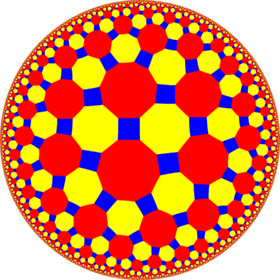 4.8.10 |
 4.8.12 |
 4.8.14 |
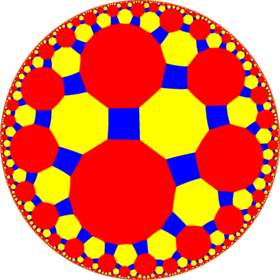 4.8.16 |
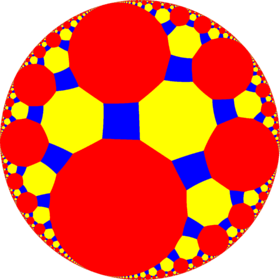 4.8.∞ |
| Omnitruncated duals |
 V4.8.4 |
 V4.8.6 |
 V4.8.8 |
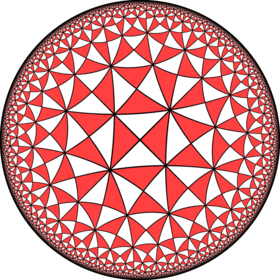 V4.8.10 |
 V4.8.12 |
 V4.8.14 |
 V4.8.16 |
 V4.8.∞ |
External links
- Olshevsky, George. "Bipyramid". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- VRML models <8>
- Conway Notation for Polyhedra Try: dP8
This article is issued from Wikipedia - version of the 6/25/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
