PDE surface
PDE surfaces are used in geometric modelling and computer graphics for creating smooth surfaces conforming to a given boundary configuration. PDE surfaces utilise partial differential equations to generate a surface which usually satisfy a mathematical boundary value problem.
PDE surfaces were first introduced into the area of geometric modelling and computer graphics by two British mathematicians, Malcolm Bloor and Michael Wilson.
Technical details
The PDE method involves generating a surface for some boundary by means of solving an elliptic partial differential equation of the form
Here  is a function parameterised by the two parameters
is a function parameterised by the two parameters  and
and 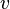 such that
such that  where
where  ,
, 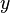 and
and 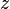 are the usual cartesian coordinate space. The boundary conditions on the function
are the usual cartesian coordinate space. The boundary conditions on the function  and its
normal derivatives
and its
normal derivatives  are imposed at the edges of the surface patch.
are imposed at the edges of the surface patch.
With the above formulation it is notable that the elliptic partial differential operator in the above PDE represents a smoothing process in which the value of the function at any point on the surface is, in some sense, a weighted average of the surrounding
values. In this way a surface is obtained as a smooth transition between
the chosen set of boundary conditions. The parameter 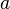 is a special design parameter which controls the relative smoothing of the surface in the
is a special design parameter which controls the relative smoothing of the surface in the  and
and 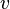 directions.
directions.
When  , the PDE is the biharmonic equation:
, the PDE is the biharmonic equation:  . The biharmonic equation is the equation produced by applying the Euler-Lagrange equation to the simplified thin plate energy functional
. The biharmonic equation is the equation produced by applying the Euler-Lagrange equation to the simplified thin plate energy functional  . So solving the PDE with
. So solving the PDE with  is equivalent to minimizing the thin plate energy functional subject to the same boundary conditions.
is equivalent to minimizing the thin plate energy functional subject to the same boundary conditions.
Applications
PDE surfaces can be utilised in many application areas. These include computer-aided design, interactive design, parametric design, computer animation, computer-aided physical analysis and design optimisation.
References
- M.I.G. Bloor and M.J. Wilson, Generating Blend Surfaces using Partial Differential Equations, Computer Aided Design, 21(3), 165-171, (1989).
- H. Ugail, M.I.G. Bloor, and M.J. Wilson, Techniques for Interactive Design Using the PDE Method, ACM Transactions on Graphics, 18(2), 195-212, (1999).
- J. Huband, W. Li and R. Smith, An Explicit Representation of Bloor-Wilson PDE Surface Model by using Canonical Basis for Hermite Interpolation, Mathematical Engineering in Industry, 7(4), 421-33 (1999).
- H. Du and H. Qin, Direct Manipulation and Interactive Sculpting of PDE surfaces, Computer Graphics Forum, 19(3), C261-C270, (2000).
- H. Ugail, Spine Based Shape Parameterisations for PDE surfaces, Computing, 72, 195--204, (2004).
- L. You, P. Comninos, J.J. Zhang, PDE Blending Surfaces with C2 Continuity, Computers and Graphics, 28(6), 895-906, (2004).
External links
- Simulation based design, DVE research (University of Bradford, UK). (A java applet demonstrating the properties of PDE surfaces)
- Dept Applied Mathematics, University of Leeds details on Bloor and Wilsons work.
