Uniformization (set theory)
In set theory, the axiom of uniformization, a weak form of the axiom of choice, states that if 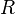 is a subset of
is a subset of  , where
, where 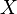 and
and 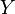 are Polish spaces,
then there is a subset
are Polish spaces,
then there is a subset  of
of 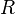 that is a partial function from
that is a partial function from 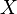 to
to 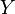 , and whose domain (in the sense of the set of all
, and whose domain (in the sense of the set of all  such that
such that  exists) equals
exists) equals
Such a function is called a uniformizing function for 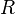 , or a uniformization of
, or a uniformization of 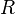 .
.

To see the relationship with the axiom of choice, observe that 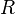 can be thought of as associating, to each element of
can be thought of as associating, to each element of 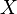 , a subset of
, a subset of 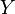 . A uniformization of
. A uniformization of 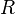 then picks exactly one element from each such subset, whenever the subset is nonempty. Thus, allowing arbitrary sets X and Y (rather than just Polish spaces) would make the axiom of uniformization equivalent to AC.
then picks exactly one element from each such subset, whenever the subset is nonempty. Thus, allowing arbitrary sets X and Y (rather than just Polish spaces) would make the axiom of uniformization equivalent to AC.
A pointclass 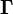 is said to have the uniformization property if every relation
is said to have the uniformization property if every relation 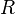 in
in 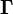 can be uniformized by a partial function in
can be uniformized by a partial function in 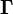 . The uniformization property is implied by the scale property, at least for adequate pointclasses of a certain form.
. The uniformization property is implied by the scale property, at least for adequate pointclasses of a certain form.
It follows from ZFC alone that  and
and  have the uniformization property. It follows from the existence of sufficient large cardinals that
have the uniformization property. It follows from the existence of sufficient large cardinals that
 and
and  have the uniformization property for every natural number
have the uniformization property for every natural number 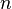 .
.- Therefore, the collection of projective sets has the uniformization property.
- Every relation in L(R) can be uniformized, but not necessarily by a function in L(R). In fact, L(R) does not have the uniformization property (equivalently, L(R) does not satisfy the axiom of uniformization).
- (Note: it's trivial that every relation in L(R) can be uniformized in V, assuming V satisfies AC. The point is that every such relation can be uniformized in some transitive inner model of V in which AD holds.)
References
- Moschovakis, Yiannis N. (1980). Descriptive Set Theory. North Holland. ISBN 0-444-70199-0.
